|
ТОПОЛОГИЧЕСКАЯ
РАЗМЕРНОСТЬ dim.
Напомним, что система подмножеств 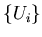 топологического
пространства топологического
пространства 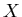 называется его покрытием, если каждая точка называется его покрытием, если каждая точка
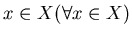 принадлежит какому-то из множеств (хотя бы
одному) принадлежит какому-то из множеств (хотя бы
одному) 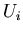 , т.е. , т.е.
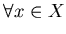
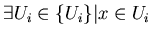 . Будем рассматривать сейчас лишь конечные покрытия. . Будем рассматривать сейчас лишь конечные покрытия.
Кратностью покрытия 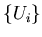 называется наибольшее из таких
чисел называется наибольшее из таких
чисел 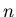
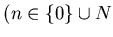 - целое неотрицательное число - целое неотрицательное число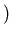 ,
что существует ,
что существует 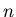 элементов покрытия элементов покрытия 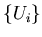 имеющих непустое
пересечение (т.е. всегда существует хотя бы (по крайней мере) одна
точка, принадлежащая имеющих непустое
пересечение (т.е. всегда существует хотя бы (по крайней мере) одна
точка, принадлежащая 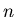 различным элементам покрытия - всем этим различным элементам покрытия - всем этим
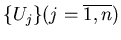 одновременно). одновременно).
Cформулируем понятие топологической размерности, восходящее к
работам Брауэра, Урысона, Менгера.
Рассмотрим для простоты компакт, т.е. замкнутое ограниченное
множество. Каждый компакт при
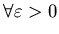 допускает допускает
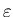 -покрытие, т.е. может быть представлен в виде
объединения конечного числа замкнутых множеств, каждое из которых
имеет диаметр -покрытие, т.е. может быть представлен в виде
объединения конечного числа замкнутых множеств, каждое из которых
имеет диаметр 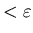 . Или из любого открытого его покрытия
всегда можно выбрать конечное подпокрытие (система множеств . Или из любого открытого его покрытия
всегда можно выбрать конечное подпокрытие (система множеств
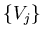 называется подпокрытием, если называется подпокрытием, если
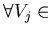 хотя бы
одному хотя бы
одному 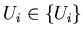 ). ).
Определение. Топологической размерностью 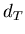 или или
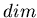 компакта компакта 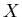 называется наименьшее из таких целых чисел называется наименьшее из таких целых чисел 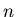 ,
что во всякое открытое покрытие пространства ,
что во всякое открытое покрытие пространства 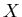 можно вписать
замкнутое подпокрытие кратности можно вписать
замкнутое подпокрытие кратности 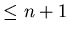 . Если таких чисел нет,
то полагается . Если таких чисел нет,
то полагается
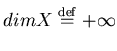 .
Топологическая размерность называется также брауэровской
размерностью или просто размерностью. .
Топологическая размерность называется также брауэровской
размерностью или просто размерностью.
Наглядный смысл этого определения довольно прост. Например, при
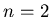 оно утверждает, что всякая двумерная ''площадка'' может быть
вымощена сколь угодно мелкими камнями (замкнутыми множествами)
так, что камни примыкают друг к другу не более чем по три
(рис.). В тоже время эта площадка не может быть вымощена сколь
угодно мелкими камнями так, чтобы были только примыкания по два.
При заполнении некоторого трехмерного объема достаточно мелкими
камнями (например кирпичной кладкой) необходимо возникают уже
примыкания по четыре. оно утверждает, что всякая двумерная ''площадка'' может быть
вымощена сколь угодно мелкими камнями (замкнутыми множествами)
так, что камни примыкают друг к другу не более чем по три
(рис.). В тоже время эта площадка не может быть вымощена сколь
угодно мелкими камнями так, чтобы были только примыкания по два.
При заполнении некоторого трехмерного объема достаточно мелкими
камнями (например кирпичной кладкой) необходимо возникают уже
примыкания по четыре.
Другим подходом к понятию размерности является идея Хаусдорфа.
|
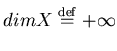 .
Топологическая размерность называется также брауэровской
размерностью или просто размерностью.
.
Топологическая размерность называется также брауэровской
размерностью или просто размерностью.
