ГЛАВА 6

Как мы уже убедились, многие регулярные фракталы строятся путем бесконечного повторения нескольких простых операций, скажем, замены одного элемента некоторой комбинацией других, ему подобных. Возникает естественный вопрос, а нельзя ли эту процедуру замены перевести на математический язык.

Так в середине 80-х годов 20 века появился метод Систем Итерируемых Функций (Iterated Function System - IFS) как простое средство получения фрактальных структур. Математические аспекты метода были разработаны Джоном Хатчинсоном, затем доработаны Майклом Барнсли, работавшем в университете штата Джорджия. Сущность этого метода на примере упомянутой выше салфетки Серпинского заключается в следующем.

Поместим исходный равносторонний треугольник с длиной стороны, равной единице, на комплексную плоскость так, как показано на рис.3.3 слева. Теперь зададимся вопросом, каким линейным преобразованием на комплексной плоскости он переводится в равносторонний треугольник в два раза меньшего размера? Ответ достаточно прост. Поскольку левое основание обоих треугольников лежит в начале координат , то функция , осуществляющая это преобразование, определяется выражением

$\begin{displaymath}t_1: f_1(z)=\displaystyle\frac12z.\eqno(1)\end{displaymath}$

Если теперь сместить этот маленький треугольник по горизонтали вправо на величину, равную , то получим преобразование , переводящее исходный треугольник в треугольник, изображенный на рис.3.4 справа. Соответствующая этому преобразованию функция , очевидно, равна

$\begin{displaymath}t_2: f_2(z)=\displaystyle\frac12z+\displaystyle\frac12.\eqno(2)\end{displaymath}$

Наконец, последний, третий треугольник получается с помощью преобразования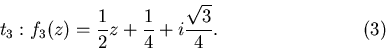

$\begin{displaymath}t_3: f_3(z)=\displaystyle\frac12z+\displaystyle\frac14+i\displaystyle\frac{\sqrt{3}}4.\eqno(3)\end{displaymath}$

В итоге линейные функции осуществляют искомое преобразование исходного треугольника в три маленьких. Если каждый из них подвергнуть трем преобразованиям, то возникнет 9 треугольников в 4 раза меньше исходного (рис.3.6).

Каждый маленький треугольник будет иметь свой генетический код , который означает, что этот треугольник был получен из исходного сначала применением преобразования , а затем к полученному было применено преобразование .

Ясно, что действуя подобным алгоритмом, мы в точности воспроизводим алгоритм построения салфетки Серпинского. Поэтому после бесконечного числа шагов мы придем в конце концов к множеству точек, образующих фрактал.

Важно заметить, что для получения точно такого же предельного результата мы могли бы стартовать с любой фигуры, необязательно имеющей форму равностороннего треугольника. Это, например, мог быть круг или квадрат или любая другая (даже несвязная) фигура, произвольным образом расположенная на плоскости.

Причина такого поведения предельно проста. Она заключается в том, что салфетка является своеобразным аттрактором для этой системы из трех линейных преобразований , называемой Системой Итерируемых Функций.

Вызывает лишь изумление, как достаточно примитивные алгоритмы приводят к столь необычным геометрическим конструкциям. Невольно он заставляет задуматься, а не закодирована ли в генах каким-нибудь схожим простым образом информация о форме и размерах существующих в природе живых организмов.

ГЛАВА 5

НАВЕРХ

ГЛАВА 7