ГЛАВА 9

 

 

ФРАКТАЛЫ И ХАОС В ДИНАМИЧЕСКИХ СИСТЕМАХ

 
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Можно ли получить фрактальные структуры из физических уравнений. Другими словами: могут ли привычные нам уравнения приводить к появлению фракталов? Ответ на этот вопрос положительный и связан, прежде всего, с одной из интенсивно развивающихся в последние 40 лет областей математической физики - динамическим хаосом.

В системах с динамическим хаосом детерминированные уравнения приводят к хаотическим решениям, хаотическим в том смысле, что в них экспоненциально быстро расходятся близлежащие первоначально траектории и возникает неустойчивость. при этом оказалось, что фракталы, как геометрические объекты, могут быть успешно применены при описании траекторий хаотических систем. Более того, можно сказать, что фракталы суть геометрические образы хаоса.

До настоящего момента мы изучали фракталы, которые являются статическими фигурами. Этот подход вполне приемлем до тех пор, пока не возникает необходимость рассмотрения таких природных явлений, как падающие потоки воды, турбулентные завихрения дыма, метеосистемы и потоки на выходе реактивных двигателей. В этих случаях один единственный фрактал соответствует моментальному снимку данного феномена. Структуры, изменяющиеся во времени, мы определяем как динамические системы. Интуитивно понятно, что динамическим соответствием фрактала является хаос. Это означает, что хаос описывает состояние крайней непредсказуемости, возникающей в динамической системе, в то время как фрактальность описывает крайнюю иррегулярность или изрезанность, присущую геометрической конфигурации.

Достаточно скоро стало ясно, что многие хаотические динамические системы, описывающие феномены окружающего нас мира, устроены очень сложно и не могут быть в полной мере представлены традиционными методами математического анализа. По-видимому, нет никакой возможности получить математические выражения для решений в замкнутом виде, даже если использовать специальные функции.

В этом направлении объектами изучения являются аттракторы динамических систем, в частности так называемые странные аттракторы.

Рассмотрим знаменитый пример, весьма наглядно демонстрирующий, что стоит за термином ''хаотическая динамика''. Эдвард Лоренц (E.N. Lorenz) из Массачусетского технологического института в 1961 году занимался численными исследованиями метеосистем, в частности моделированием конвекционных потоков в атмосфере. Он исследовал следующую систему дифференциальных уравнений:

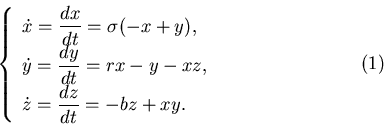
\begin{displaymath}\left\{\begin{array}{lcl} \dot{x}=\displaystyle\frac{dx}{dt}=... ...\displaystyle\frac{dz}{dt}=-bz+xy. \end{array} \right. \eqno(1)\end{displaymath}

Где $\sigma, r, b$ - постоянные положительные параметры. Системе Лоренца присуща существенная зависимость от начальных условий - основная черта хаотической динамики. Существенную зависимость иногда называют эффектом бабочки. Такое название относится к невозможности делать долгосрочные прогнозы погоды.

Проиллюстрируем на примерах, что подразумевается под аттрактором дифференциального уравнения. Кроме того, найдем фрактальную размерность аттракторов конкретных дифференциальных уравнений или приведем оценку этой размерности.

Пример 1. Пусть дана система уравнений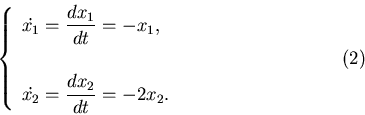

\begin{displaymath}\left\{ \begin{array}{lcl} \dot{x_1}=\displaystyle\frac{dx_1}... ...isplaystyle\frac{dx_2}{dt}=-2x_2.\\ \end{array}\right.\eqno(2)\end{displaymath}

Общее решение этой системы задается формулами

\begin{displaymath}x_1(t)=c_1\cdot e^{-t}, x_2(t)=c_2\cdot e^{-2t}, c_1, c_2=const.\eqno(3)\end{displaymath}

Если заданы начальные условия $x_1(0)$ и $x_2(0)$, то траектория (то есть решение системы (2)), выходящая из этой точки, задается формулами

\begin{displaymath}x_1(t)=e^{-t}\cdot x_1(0), x_2(t)=e^{-2t}\cdot x_2(0).\end{displaymath}

Очевидно, любая траектория при $t\to+\infty$ стремится к точке $(0,0)$. В этом простейшем случае говорят, что точка $(0,0)$ является аттрактором $A$ системы (2) (или решений системы (2)): $A=(0,0)$. Фрактальная размерность аттрактора $A$ $d_F(A)=0$.

Пример 2. Аттрактор, являющийся предельным циклом.

Пусть дана система двух дифференциальных уравнений, которая в полярных координатах $(\rho,\varphi)$ на плоскости ${\cal R}^2$ имеет вид:

\begin{displaymath}\dot{\rho}=\rho(1-\rho), \eqno(4)\end{displaymath}


\begin{displaymath}\dot{\varphi}=1.\eqno(5)\end{displaymath}

Из уравнения (5) следует, что

\begin{displaymath}\varphi(t)=t+c_1.\eqno(6)\end{displaymath}

Легко видеть, что окружность

\begin{displaymath}\rho(t)=1\eqno(7)\end{displaymath}

является решением уравнения (4). Действительно $\dot{\rho}=0$ и правая часть уравнения (4) при $\rho=1$ обращается в нуль: $\rho(1-\rho^2)\vert\rho=1=0$.

Таким образом, окружность (6), (7) является решением системы (4), (5), и притом периодическим с периодом $2\pi$. Действительно, полярная координата $\varphi$ обладает этим свойством: точки с полярными координатами $(1,\varphi)$ и $(1,\varphi+2\pi)$ изображают одну и туже точку на окружности $\rho=1$.

Теперь заметим, что если $(\rho(t),\varphi(t))$ - решение системы (4), (5) и $0<\rho(t)<1$, то из уравнения (4) следует, что $\dot{\rho}(t)=\rho(t)\cdot(1-{(\rho(t))}^2)>0$, то есть функция $\rho(t)$ возрастает, приближаясь к значению $\rho=1$, а траектория $(\rho(t),\varphi(t))=(\rho(t),t+c_1)$ совершает спиралеобразное движение внутри окружности $\rho=1$ (рис.).

Если же решение $(\rho_1(t),\varphi(t))=(\rho_1(t),t+c_1)$ в некоторый момент $t$ имеет $\rho_1(t)>1$, то, согласно уравнению (4), $\dot{\rho_1}(t)=\rho_1(t)\cdot(1-{(\rho_1(t))}^2)<0$ и $\rho_1(t)$ убывает с возрастанием $t$. В этом случае кривая $(\rho_1(t),t+c_1)$ спиралеобразно приближается при $t\to+\infty$ к окружности $\rho=1$ извне этой окружности.

Таким образом, решения $(\rho(t),\varphi(t)$ системы, находящиеся вне и внутри окружности, и сама окружность имеют вид, изображенный на рис.5.1.

Мы показали, что все траектории системы уравнений (кроме начала координат $\rho=0$, являющегося неподвижной точкой системы (4), (5)) притягиваются (стремятся) при $t\to+\infty$ к окружности $\{\rho=1\}=A$. Поэтому эта окружность называется предельным циклом системы (4), (5). Такой предельный цикл (притягивающий) называют аттрактором системы (4), (5). Фрактальная размерность этого аттрактора равна 1: $d_F(A)=1$.

Пример 3. Оценка фрактальной размерности аттрактора системы уравнений Лоренца.

Вернемся к системе (1). можно показать, что любые решения $u(t)=(x(t),y(t),z(t))$ системы () при $t\geq0$ ограничены в трехмерном пространстве. Точнее имеет место оценка:

\begin{displaymath}\vert u(t)\vert^2\leq e^{-2lt}\cdot\vert u(0)\vert^2+c\cdot(1-e^{-2lt}),\eqno(8)\end{displaymath}

где $\vert u\vert^2=\vert x\vert^2+\vert y\vert^2+\vert z\vert^2$, $l=\min(1,\sigma)$, $c$ - некоторая постоянная, выражающаяся через $l,b$ и $\sigma$. Из (8) следует, что при ограниченных начальных условиях $\vert u(0)\vert\leq M$, траектории (решения) $u(t)$ системы (1) выходящие из $u(0)$ ограничены при всех $t\geq 0$:

\begin{displaymath}\vert u(t)\vert^2\leq R(M)=M^2+c, \forall t\geq0.\eqno(9)\end{displaymath}

Следуя общей теории аттракторов дифференциальных уравнений из (8), (9) выводится, что система уравнений Лоренца (1) обладает аттрактором $A$ (рис5.2). Точнее, существует такое замкнутое ограниченное множество $A$ в ${\cal R}^3$, которое притягивает любые семейства траекторий системы (1). Это означает, что при $\vert u(0)\vert^2\leq M_1$ (где $M_1$ любая фиксированная константа) соответствующее таким $\{u(0)\}$ семейство траекторий $\{u(t)\}$ при $t\to+\infty$ равномерно стремится к множеству $A$, называемому аттрактором: $\{u(t)\}\to A$ при $t\to+\infty$. Доказано, что например при значениях $\sigma=10, r=28, b=8/3$ фрактальная размерность

\begin{displaymath}d_F(A)\leq 2,538\dots\end{displaymath}

В таких ситуациях (то есть при большом дробном значении фрактальной размерности аттрактора) говорят, что наблюдается явление турбулентности.

Пример 4. Модель Энона. (Henon M.).

Модель (отображение) Энона с дискретным временем задается системой: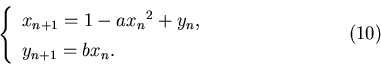

\begin{displaymath}\left\{ \begin{array}{lcl} x_{n+1}=1-a{x_n}^2+y_n,\\ y_{n+1}=bx_n. \end{array} \right. \eqno(10)\end{displaymath}

Здесь $x_n$ и $y_n$ - динамические переменные, $n$ играет роль времени, $a,b$ - параметры системы. Эта модель может быть получена при рассмотрении динамики ротатора с затуханием при воздействии на него периодических толчков.

Оказалось, что, начиная с некоторых критических значений коэффициентов $a$ и $b$, в системе возникает хаотическая динамика, а сами полученные наборы точек обнаруживают самоподобную структуру (рис.5.4). На рис.5.4,а показан весь аттрактор Энона при начальных условиях $x_0=1,0$ $y_0=-0,1$. Выделенный на рис.5.4,а прямоугольник дан в увеличенном виде на рис.5.4,б. Он как бы состоит из трех групп, каждая из которых содержит три, две и одну линии. Еще раз повторив процедуру увеличения убеждаемся в существовании самоподобия аттрактора Энона (рис.5.3).

Этот аттрактор имеет дробную размерность

\begin{displaymath}d_F(A)\approx 1,26\dots\end{displaymath}

при выбранных нами условиях.

 

 

 

Главная - Введение - Основные понятия - Размерности - Самоподобие

Л-системы - СИФ (IFS) - Мультифракталы - Комплексная динамика - Фракталы и хаос

Чтиво - Фракталы в Интернете - Программы - Галерея - Скачать - В заключение  

 

Copyright © 2002-2004

Ринчино Андрей

 
Hosted by uCoz