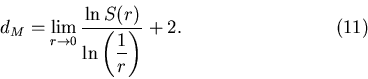|
|
РАЗМЕРНОСТЬ
МИНКОВСКОГО dM.
Размерность Минковского может служить аналогом размерности
Хаусдорфа-Безиковича, удобным для использования в прикладных
задачах. Эти размерности как правило совпадают, но алгоритм
определения размерности Минковского несколько проще.
Определение размерности Минковского (Герман Минковский) 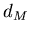 для
кривой (фрактальной или гладкой) в общих чертах сводится к
следующему. Пусть центр небольшого евклидова шара (круга) радиуса для
кривой (фрактальной или гладкой) в общих чертах сводится к
следующему. Пусть центр небольшого евклидова шара (круга) радиуса
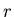 движется вдоль кривой, заметая площадь Минковского, то
есть площадь движется вдоль кривой, заметая площадь Минковского, то
есть площадь 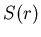 , возникающей при движении шара. Разделим
площадь , возникающей при движении шара. Разделим
площадь 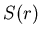 на на 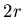 и устремим и устремим 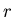 к нулю. В случае гладкой
кривой мы получили бы в пределе длину кривой, но для фрактальной
кривой результат бесконечный. Действительно, отношение к нулю. В случае гладкой
кривой мы получили бы в пределе длину кривой, но для фрактальной
кривой результат бесконечный. Действительно, отношение 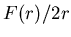 пропорционально величине
пропорционально величине 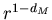 , которая при , которая при 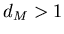 расходится для
расходится для 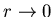 . Значение величины . Значение величины 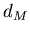 служит мерой
скорости расхождения и называется размерностью
Минковского-Булигана. Ее можно вычислить по формуле: служит мерой
скорости расхождения и называется размерностью
Минковского-Булигана. Ее можно вычислить по формуле:
В случае гладкой кривой 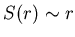 и и 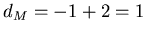 , как и
следовало ожидать. , как и
следовало ожидать.
Для всех строго самоподобных фракталов размерность Минковского
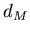 равна размерности Хаусдорфа-Безиковича равна размерности Хаусдорфа-Безиковича 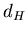 . Если эти
размерности не совпадают, то . Если эти
размерности не совпадают, то
Это говорит о
том, что размерность Минковского несколько ''грубее'' размерности
Хаусдорфа-Безиковича, так как не учитывает некоторые тонкие
структуры объекта.
|