ГЛАВА 8

 

 

КОМПЛЕКСНАЯ ДИНАМИКА

 
 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

В 1879 году Артур Кэли поставил задачу итерирования комплексных функций, которая позднее стимулировала исследования Гастона Жюлиа по проблемам теории множеств, названных теперь его именем. Проблема Кэли заключается в исследовании сходимости классического алгоритма Ньютона нахождения кубических корней, но при условии, что вещественные числа заменяются на комплексные.

Метод Ньютона для нахождения вещественного корня 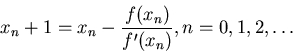$f(x)$ (его также часто называют методом касательных) заключается в следующем. Выберем начальное приближение $x_0$, вычислим точки

\begin{displaymath}x_n+1=x_n-\displaystyle\frac{f(x_n)}{f'(x_n)}, n=0,1,2,\dots\end{displaymath}

и найдем предел $\lim_{n\to\infty}x_n$. Предполагается, что $f, f', f''$ существуют и непрерывны в окрестности нуля, скажем при $x=c$. Если $x_0$ находится достаточно близко к $c$ и если $f'(c)\neq0$, то

\begin{displaymath}\lim_{n\to\infty}x_n=c.\end{displaymath}

Этот метод не менее эффективен и для комплексных чисел. Это значит, что, стартовав в непосредственной близости от значения корня уравнения 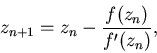$f(z)=0$, мы используя итерационный алгоритм

\begin{displaymath}z_{n+1}=z_n-\displaystyle\frac{f(z_n)}{f'(z_n)},\end{displaymath}

получим последовательность комплексных чисел, быстро сходящуюся к этому корню. возникает правомерный вопрос, а что будет, если начальная точка $z_0$ выбрана в плоскости комплексных чисел не вблизи от корня, а произвольным образом?

Для $f(x)=x^3-1$ нули равны кубическим корням из 1, и итерации Ньютона принимают вид:

\begin{displaymath}x_{n+1}=x_n-\displaystyle\frac{{x_n}^3-1}{3{x_n}^2}.\end{displaymath}

Кэли предположил исследовать поведение этих итераций для комплексных 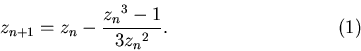$z_n$:

\begin{displaymath}z_{n+1}=z_n-\displaystyle\frac{{z_n}^3-1}{3{z_n}^2}.\eqno(1)\end{displaymath}

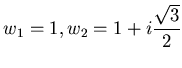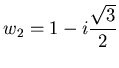Имеются три кубических корня из 1, а именно, $w_1=1, w_2=1+i\displaystyle\frac{\sqrt{3}}{2}$ и $ w_2=1-i\displaystyle\frac{\sqrt{3}}{2}$. Область притяжения для корня $w_i$ есть множество $A(w_i)=\{z\in C\vert$ если $z_0=z$, то $\lim_{n\to\infty}z_n=w_i\}$.

Кэли поставил задачу описания областей $A(w_1),A(w_2),A(w_3)$.

Уравнение (1) является результатом итерирования функции

\begin{displaymath}g(z)=z-\displaystyle\frac{f(z)}{f'(z)}.\eqno(2)\end{displaymath}

Нули $f(z)$ являются неподвижными точками $g(z)$, и так как

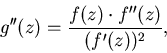
\begin{displaymath}g''(z)=\displaystyle\frac{f(z)\cdot f''(z)}{(f'(z))^2},\end{displaymath}

они сверхпритягивающие.

Как и в случае вещественных итераций, если начальная точка $z_0$ находится достаточно близко к корню $w_i$, то ньютоновские итерации сходятся к этому корню. Таким образом, каждая область $A(w_i)$ содержит окрестность $w_i$. Но какую часть комплексной плоскости занимает $A(w_i)$ и какова ее геометрия? Ответ на этот вопрос крайне нетривиален.

Рассмотрим соответствующую задачу для квадратных корней. В этом случае 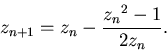$f(z)=z^2-1$ и ньютоновские итерации имеют вид:

\begin{displaymath}z_{n+1}=z_n-\displaystyle\frac{{z_n}^2-1}{2z_n}.\end{displaymath}

Если $z_n$ лежит в правой полуплоскости, то $z_n\to+1$ при $n\to\infty$, а если в левой полуплоскости, то $z_n\to-1$ при $n\to\infty$. Таким образом, за исключением начальных точек $z_0$, которые равноудалены от двух корней, $z_n$ сходятся к корню, ближайшему к $z_0$. Если $z_0$ лежит на мнимой оси, то в этом случае итерации не сходятся.

По аналогии со случаем $z^2-1$ можно предположить, что в случае $z^3-1$ итерированные значения $z_n$, вычисленные по формуле (1), сходятся к кубическому корню, ближайшему к $z_0$, если такой ближайший корень существует. Таким образом, ответ на вопрос Кэли предположительно выглядит как пирог, разделенный на три равные части (рис.1). Как ни странно, это предположение неверно.

 

 

Теорема. Пусть $g(z)=z-(z^3-1)/(3z^2)$ - функция Ньютона для $z^3-1$. Тогда множество Жюлиа для $g$ имеет вид:

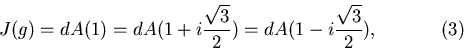
\begin{displaymath}J(g)=dA(1)=dA(1+i\displaystyle\frac{\sqrt{3}}{2})=dA(1-i\displaystyle\frac{\sqrt{3}}{2}),\eqno(3)\end{displaymath}

то есть 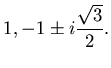$J(g)$ является границей каждой из областей притяжения для трех притягивающих неподвижных точек: $1, -1\pm i\displaystyle\frac{\sqrt{3}}{2}.$

Терема говорит нам о том, что ответ на вопрос Кэли отличается от того, что изображено на рис.1. Кроме начала координат точки на границе любой области притяжения имеют малые окрестности, пересекающиеся ровно с двумя областями. Но выражение (3) говорит о том, что в произвольной окрестности каждой граничной точки любой из этих областей должны находится точки, принадлежащие всем трем областям. Правильное изображение трех бассейнов притяжения для $g(z)$ было получено только с помощью компьютера (рис.).

Граница областей притяжения состоит из сильно переплетенных самоподобных фрактальных структур.

Иными словами можно задать вопрос: как закрасить плоскость тремя красками, чтобы на границе каждой цветной области существовали точки двух других цветов, которые были бы расположены произвольно близко? Ответ мы получим, раскрасив области притяжения для $g(z)$ разными красками.

 

 

ГЛАВА 7

 НАВЕРХ ГЛАВА 9

Главная - Введение - Основные понятия - Размерности - Самоподобие

Л-системы - СИФ (IFS) - Мультифракталы - Комплексная динамика - Фракталы и хаос

Чтиво - Фракталы в Интернете - Программы - Галерея - Скачать - В заключение  

 

Copyright © 2002-2004

Ринчино Андрей

 
Hosted by uCoz