|
|
Фракталы естественным образом возникают при комплексных
преобразованиях плоскости, сопоставляющих одному комплексному
числу другое комплексное число. К примеру, рассмотрим комплексный
полином 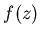 степени степени 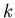 . Его можно трактовать как комплексное
преобразование плоскости - отображение . Его можно трактовать как комплексное
преобразование плоскости - отображение 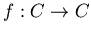 , задаваемое
формулой , задаваемое
формулой 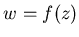 . Это отображение можно итерировать, рассматривая
бесконечную последовательность степеней . Это отображение можно итерировать, рассматривая
бесконечную последовательность степеней 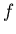 , т.е. , т.е. 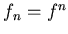 , где , где
Пусть 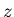 -
произвольная точка плоскости. Применяя к ней бесконечную
последовательность преобразований -
произвольная точка плоскости. Применяя к ней бесконечную
последовательность преобразований 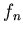 мы получаем бесконечную
последовательность точек мы получаем бесконечную
последовательность точек
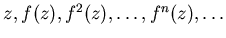 Другими словами, мы рассматриваем орбиту точки
Другими словами, мы рассматриваем орбиту точки 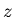 при действии на
нее итерациями отображения при действии на
нее итерациями отображения 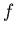 . Удобно рассматривать пополненную
комплексную плоскость . Удобно рассматривать пополненную
комплексную плоскость 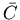 (сферу Римана). Тогда бесконечная
последовательность точек обязательно имеет предельные точки на
сфере. (сферу Римана). Тогда бесконечная
последовательность точек обязательно имеет предельные точки на
сфере.
Мы скажем, что некоторое подмножество 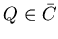 инвариантно
относительно отображения инвариантно
относительно отображения 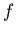 , если оно переходит в себя при
действии всех итераций , если оно переходит в себя при
действии всех итераций
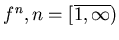 .
Оказывается, такие множества часто являются фракталами. .
Оказывается, такие множества часто являются фракталами.
Т.к. 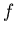 - комплексный полином, то отображение - комплексный полином, то отображение 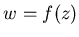 всегда
имеет неподвижные точки. Они определяются, как корни уравнения всегда
имеет неподвижные точки. Они определяются, как корни уравнения
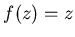 , т.е. , т.е. 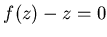 . Если степень полинома . Если степень полинома 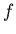 равна равна 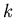 , то
это уравнение имеет ровно , то
это уравнение имеет ровно 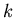 корней (некоторые корни могут быть
кратными). Корни изображаются точками корней (некоторые корни могут быть
кратными). Корни изображаются точками
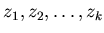 на на
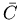 . Пусть в какой-то из этих точек . Пусть в какой-то из этих точек 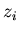 выполнено
неравенство выполнено
неравенство
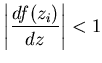 .
Тогда отображение .
Тогда отображение 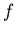 является сжимающим в этой точке, т.е. корень является сжимающим в этой точке, т.е. корень
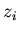 является точкой притяжения других точек. Можно далее
рассмотреть на плоскости область притяжения корня является точкой притяжения других точек. Можно далее
рассмотреть на плоскости область притяжения корня 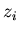 , т.е.
совокупность точек , т.е.
совокупность точек 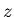 для которых для которых
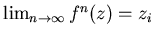 .
Область начальных значений, из которых итерации приводят к одному
и тому же корню называется бассейном корня. Оказывается
такие множества также часто являются фракталами. Множество .
Область начальных значений, из которых итерации приводят к одному
и тому же корню называется бассейном корня. Оказывается
такие множества также часто являются фракталами. Множество
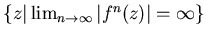 - область притяжения
бесконечно удаленной точки - тоже фрактал. - область притяжения
бесконечно удаленной точки - тоже фрактал.
|