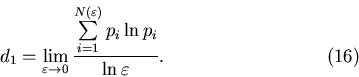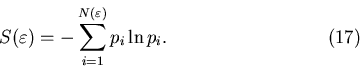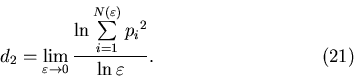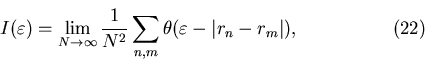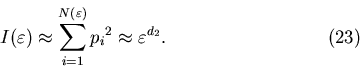|
|
7.1. Мультифракталы
Мультифракталы - неоднородные фрактальные объекты для полного
описания которых,в отличие от регулярных фракталов,
недостаточно введения всего лишь одной величины, его фрактальной размерности 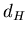 , а
необходим целый спектр таких размерностей, число которых, вообще
говоря, бесконечно. Причина этого заключается в том, что наряду с
чисто геометрическими характеристиками, определяемыми величиной , а
необходим целый спектр таких размерностей, число которых, вообще
говоря, бесконечно. Причина этого заключается в том, что наряду с
чисто геометрическими характеристиками, определяемыми величиной
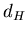 , такие фракталы обладают и некоторыми статистическими
свойствами. , такие фракталы обладают и некоторыми статистическими
свойствами.
Проще всего пояснить, что понимается под ''неоднородным
фракталом'' на примере треугольника Серпинского, построенного с
помощью СИФ. Мы показали, что система итерируемых функций для
этого фрактала состоит из трех преобразований на комплексной
плоскости, каждое из которых выбиралось с одинаковой вероятностью,
равной 1/3. В результате мы получили рис.2.5.
Допустим, однако, что в методе случайных итераций мы теперь по
какой-то причине отдали предпочтение одной из вершин треугольника
и стали выбирать ее с вероятностью 90 %.
Две же остальные вершины равноценны и на их долю приходится по 5 % (рис.7.1, 7.2).
Видно, что точки внутри треугольника распределены теперь крайне
неравномерно. Тем не менее по обычной терминологии данное
множество точек является фракталом, так как сохранилось основное
свойство фрактала - самоподобие.
Однако несмотря на неравномерность распределения точек по
фракталу, его фрактальная размерность осталась при этом прежней,
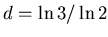 . Покрытие этого множества все более и более мелкими
треугольниками можно осуществить по тому же алгоритму, что и
ранее. Такое совпадение заставляет нас заняться поиском иных
количественных характеристик, которые могли бы отличить
неравномерное распределение точек от равномерного. . Покрытие этого множества все более и более мелкими
треугольниками можно осуществить по тому же алгоритму, что и
ранее. Такое совпадение заставляет нас заняться поиском иных
количественных характеристик, которые могли бы отличить
неравномерное распределение точек от равномерного.
7.2. Обобщенные размерности Реньи 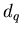
Дадим теперь общее определение мультифракталов. Рассмотрим
фрактальный объект, занимающий некую ограниченную область 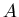 ,
имеющую ,
имеющую 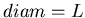 в евклидовом пространстве размерности в евклидовом пространстве размерности 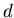 .
Пусть на каком-то этапе его построения он представляет собой
множество из .
Пусть на каком-то этапе его построения он представляет собой
множество из 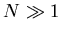 , как-то распределенных в этой области. В
конце концов предполагаем, что , как-то распределенных в этой области. В
конце концов предполагаем, что 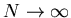 . .
Множество точек может представлять собой некоторую популяцию,
состоящую из особей одного вида распределенных по области 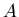 .
Такой популяцией могут быть, например, народонаселение или сеть
метеостанций. Обе популяции неравномерно распределены по
поверхности Земли. Пространственное распределение энергии,
распределение ошибок в канале связи, распределение примесей в
жидких средах, масс в веществе - примеры таких популяций. Важно
отметить, что неравномерное распределение особей остается в силе
независимо от линейного масштаба. .
Такой популяцией могут быть, например, народонаселение или сеть
метеостанций. Обе популяции неравномерно распределены по
поверхности Земли. Пространственное распределение энергии,
распределение ошибок в канале связи, распределение примесей в
жидких средах, масс в веществе - примеры таких популяций. Важно
отметить, что неравномерное распределение особей остается в силе
независимо от линейного масштаба.
Разобьем всю область 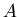 на гиперкубические ячейки со стороной на гиперкубические ячейки со стороной
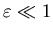 и объемом и объемом 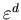 соответственно. Далее
нас будут интересовать только занятые ячейки, в которых содержится
хотя бы одна точка. Обозначим соответственно. Далее
нас будут интересовать только занятые ячейки, в которых содержится
хотя бы одна точка. Обозначим
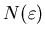 число таких ячеек,
оно очевидно зависит от число таких ячеек,
оно очевидно зависит от 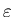 . Пусть . Пусть
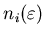 -
число точек в -
число точек в 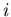 -й ячейке. Тогда величина -й ячейке. Тогда величина
- есть вероятность того, что некоторая точка содержится в 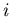 -м
кубике. То есть эта вероятность характеризует относительную
заселенность ячейки. По правилу нормировки вероятностей: -м
кубике. То есть эта вероятность характеризует относительную
заселенность ячейки. По правилу нормировки вероятностей:
Введем в рассмотрение так называемую обобщенную
статистическую сумму, характеризуемую показателем 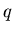 : :
где
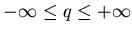 . .
Определение. Спектром обобщенных фрактальных
размерностей Реньи, характеризующих распределение точек в области
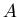 называется совокупность величин: называется совокупность величин:
где
Для обычного однородного фрактала все эти размерности совпадают.
То есть если 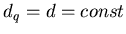 , т.е. не зависит от , т.е. не зависит от 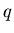 , то рассматриваемое
множество точек представляет собой обычный, регулярный фрактал,
который характеризуется всего лишь одной величиной - фрактальной
размерностью , то рассматриваемое
множество точек представляет собой обычный, регулярный фрактал,
который характеризуется всего лишь одной величиной - фрактальной
размерностью 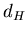 . Напротив, если функция . Напротив, если функция 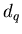 как-то меняется с как-то меняется с
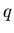 , то рассматриваемое множество точек является мультифракталом. , то рассматриваемое множество точек является мультифракталом.
Таким образом, мультифрактал в общем случае характеризуется
нелинейной функцией 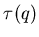 ,определяющей поведение
статистической суммы ,определяющей поведение
статистической суммы
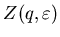 при при
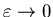
Следует иметь ввиду, что предельный нереход при
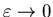 надо выполнять, помня, что ему всегда предшествует предел
надо выполнять, помня, что ему всегда предшествует предел
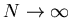 . .
Покажем теперь, как ведет себя обобщенная статистическая сумма в
случае обычного регулярного фрактала с фрактальной размерностью
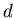 . В этом случае во всех занятых ячейках сдержится одинаковое
количество точек . В этом случае во всех занятых ячейках сдержится одинаковое
количество точек
то есть
фрактал является однородным. Тогда очевидно, что относительные
населенности всех ячеек
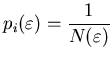 тоже
одинаковы и обобщенная статистическая сумма принимает вид: тоже
одинаковы и обобщенная статистическая сумма принимает вид:
Учтем теперь, что,
согласно определению фрактальной размерности 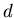 , число занятых
ячеек при достаточно малом , число занятых
ячеек при достаточно малом 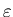 ведет себя следующим
образом: ведет себя следующим
образом:
Подставляя это в формулу (8) и сравнивая с (6), мы приходим к
выводу, что в случае обычного фрактала функция
т.е. является линейной. Тогда все
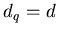 и действительно не зависят от и действительно не зависят от 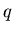 . Для фрактала, все
обобщенные фрактальные размерности . Для фрактала, все
обобщенные фрактальные размерности 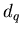 которого совпадают, часто
используется термин монофрактал. которого совпадают, часто
используется термин монофрактал.
Если распределение точек по ячейкам неодинаково, то фрактал
является неоднородным, т.е. представляет из себя мультифрактал, и
для его характеристики необходим целый спектр обобщенных
фрактальных размерностей 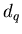 , число которых, в общем случае,
бесконечно. , число которых, в общем случае,
бесконечно.
Так, например, при 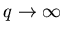 основной вклад в обобщеннную
статистическую сумму (3) вносят ячейки, содержащие наибольшее
число частиц основной вклад в обобщеннную
статистическую сумму (3) вносят ячейки, содержащие наибольшее
число частиц 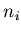 в них и, следовательно, характеризующиеся
наибольшей вероятностью их заполнения в них и, следовательно, характеризующиеся
наибольшей вероятностью их заполнения 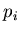 . Наоборот, при . Наоборот, при 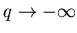 оcновной вклад в сумму (3) дают самые разреженные ячейки
с малыми значениями чисел заполнения оcновной вклад в сумму (3) дают самые разреженные ячейки
с малыми значениями чисел заполнения 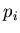 . Таким образом, функция . Таким образом, функция
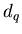 показывает, насколько неоднородным является исследуемое
множество точек показывает, насколько неоднородным является исследуемое
множество точек 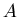 . .
7.3. Фрактальная размерность 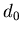 и информационная
размерность и информационная
размерность 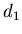 . .
Выясним теперь, какой физический смысл имеют обобщенные
фрактальные размерности 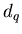 для некоторых конкретных значений для некоторых конкретных значений
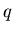 . Так, при . Так, при 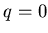 из выражения (3) следует, что из выражения (3) следует, что
С другой стороны,
согласно формулам (6) и (4),
Сопоставляя эти два равенства, мы приходим к соотношению
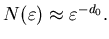 Это означает, что
величина Это означает, что
величина 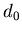 представляет собой обычную хаусдорфову размерность
множества представляет собой обычную хаусдорфову размерность
множества 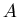 . Она является наиболее грубой характеристикой
мультифрактала и не несет информации о его статистических
свойствах. . Она является наиболее грубой характеристикой
мультифрактала и не несет информации о его статистических
свойствах.
Выясним теперь смысл величины 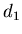 . Поскольку при . Поскольку при 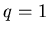 в силу
условия нормировки вероятности (2), статистическая сумма равна в силу
условия нормировки вероятности (2), статистическая сумма равна
то 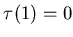 . Таким образом, мы
имеем неопределенность в выражении (4) для . Таким образом, мы
имеем неопределенность в выражении (4) для 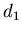 . Раскроем эту
неопределенность с помощью очевидного равенства . Раскроем эту
неопределенность с помощью очевидного равенства
Теперь, устремляя 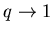 ,
раскладывая экспоненту и учитывая условие нормировки (2), получаем ,
раскладывая экспоненту и учитывая условие нормировки (2), получаем
В
результате мы приходим к следующему выражению
С точностью до знака числитель в этой формуле представляет собой
энтропию
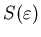 фрактального множества: фрактального множества:
Такое определение энтропии множества полностью
идентично используемому в термодинамиаке, где под 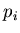 понимается
вероятность обнаружить систему в квантовом состоянии понимается
вероятность обнаружить систему в квантовом состоянии 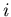 . В
результате величина обобщенной фрактальной размерности . В
результате величина обобщенной фрактальной размерности 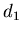 связана с энтропией
связана с энтропией
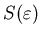 соотношением соотношением
В термодинамике энтропия есть мера беспорядка в системе.
Поскольку, как следует из (18),
то величина
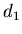 характеризует информацию, необходимую для определения
местоположения точки в некоторой ячейке. В связи с этим обобщенную
фрактальную размерность характеризует информацию, необходимую для определения
местоположения точки в некоторой ячейке. В связи с этим обобщенную
фрактальную размерность 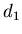 часто называют информационной
размерностью. Она показывает, как информация, необходимая для
определения местоположения точки, возрастает при стремлении
размера ячейки часто называют информационной
размерностью. Она показывает, как информация, необходимая для
определения местоположения точки, возрастает при стремлении
размера ячейки 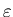 к нулю. к нулю.
7.4. Корреляционная размерность 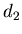
Рассмотрим еще один частный случай, 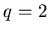 , и покажем, какой
физический смысл имеет обобщенная фрактальная размерность , и покажем, какой
физический смысл имеет обобщенная фрактальная размерность 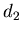 .
Для нее справедливо следующее выражение .
Для нее справедливо следующее выражение
Определим парный корреляционный интеграл
где суммирование производится по всем парам точек нашего
фрактального множества с радиус-векторами 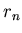 и и 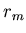 ; ;
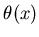 - ступенчатая функция Хевисайда, - ступенчатая функция Хевисайда, 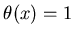 , если , если
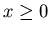 и и 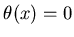 , если , если 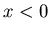 . Сумма в выражении (22)
определяет число пар точек . Сумма в выражении (22)
определяет число пар точек 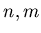 для которых расстояние между ними
меньше, чем для которых расстояние между ними
меньше, чем 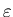 . Поэтому, поделенная на . Поэтому, поделенная на 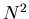 , она
определяет вероятность того, что две наугад взятые точки разделены
расстоянием меньшим, чем , она
определяет вероятность того, что две наугад взятые точки разделены
расстоянием меньшим, чем
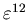 . .
Эту же верятность можно определить по-другому. Величина 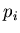 согласно своему определению (1), представляет собой вероятность
попадания точки в
согласно своему определению (1), представляет собой вероятность
попадания точки в 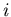 -ю ячейку с размером -ю ячейку с размером 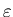 .
Следовательно, величина .
Следовательно, величина 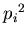 представляет собой вероятность
попадания в эту ячейку двух точек. Суммируя представляет собой вероятность
попадания в эту ячейку двух точек. Суммируя 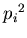 по всем
занятым ячейкам, мы получаем вероятность того, что две произвольно
выбранные точки из множества по всем
занятым ячейкам, мы получаем вероятность того, что две произвольно
выбранные точки из множества 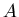 лежат внутри одной ячейки с
размером лежат внутри одной ячейки с
размером 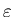 . Следовательно, расстояние между этими
точками будет меньше или порядка . Следовательно, расстояние между этими
точками будет меньше или порядка 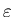 . Таким образом, с
точностью до численных коэффициентов, принимая во внимание
равенство (21), получаем . Таким образом, с
точностью до численных коэффициентов, принимая во внимание
равенство (21), получаем
Мы приходим к выводу, что обобщенная размерность 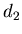 определяет
зависимость корреляционного интеграла определяет
зависимость корреляционного интеграла
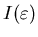 от от
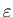 в пределе в пределе
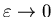 . По этой причине
величину . По этой причине
величину 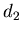 обычно называют корреляционной размерностью. обычно называют корреляционной размерностью.
|

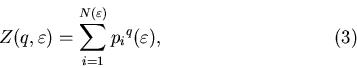

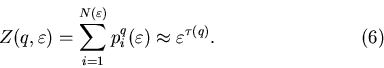

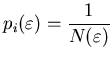 тоже
одинаковы и обобщенная статистическая сумма принимает вид:
тоже
одинаковы и обобщенная статистическая сумма принимает вид:
![\begin{displaymath}Z(q,\varepsilon)=\sum_{i=1}^{N(\varepsilon)}p_i^q=\sum_{i=1}^{N(\varepsilon)}p_i\cdot
\exp [(q-1)\ln p_i ].\eqno(14)\end{displaymath}](../HTML/multifractal/img72.gif)
![\begin{displaymath}Z(q\to1,\varepsilon)\approx\sum_{i=1}^{N(\varepsilon)}[p_i+(q...
...n
p_i]=1+(q-1)\sum_{i=1}^{N(\varepsilon)} p_i \ln p_i.\eqno(15)\end{displaymath}](../HTML/multifractal/img74.gif)