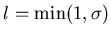|
|
Нередко то, что мы наблюдаем в природе, интригует нас бесконечным
повторением одного и того же узора, увеличенного или уменьшенного
во сколько угодно раз. Например, у дерева есть ветви. На этих
ветвях есть ветки поменьше и т.д. Теоретически, элемент
''разветвление'' повторяется бесконечно много раз, становясь все
меньше и меньше. То же самое можно заметить, разглядывая
фотографию горного рельефа. Так появляется характерное для
фракталов свойство самоподобия. Даже в случае достаточно сложных
фракталов, таких, как граница множества Мандельброта, когда чистое
самоподобие отсутствует, имеется почти полное повторение базовой
формы во все более и более уменьшенном виде.
Как уже упоминалось, во многих работах по фракталам самоподобие
используется в качестве определяющего свойства.
Рассмотрим, к примеру, отрезок прямой конечной длины. Разделим
отрезок на 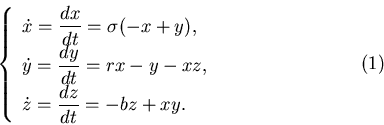 равных частей. Тогда каждую часть можно считать
копией всего отрезка, уменьшенной в равных частей. Тогда каждую часть можно считать
копией всего отрезка, уменьшенной в  раз. Очевидно, раз. Очевидно,  и и 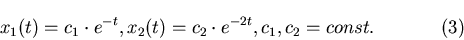 связаны соотношением
связаны соотношением 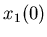 (рис.1.4). Если квадрат разбить
на (рис.1.4). Если квадрат разбить
на 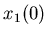 равных квадратов (с площадью, в равных квадратов (с площадью, в 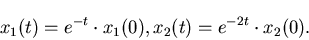 раз меньше площади
исходного), то соотношение запишется как раз меньше площади
исходного), то соотношение запишется как 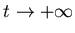 . Если куб
разбить на . Если куб
разбить на  равных кубов (с объемом, в равных кубов (с объемом, в  раз меньше
объема исходного), то соотношение примет следующий вид: раз меньше
объема исходного), то соотношение примет следующий вид:  . Заметим, что размерность . Заметим, что размерность 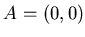 объекта, будь то отрезок,
квадрат или куб, проявляется как степень объекта, будь то отрезок,
квадрат или куб, проявляется как степень  в соотношении между в соотношении между
 числом равных подобъектов, и коэффициентом подобия числом равных подобъектов, и коэффициентом подобия  . А
именно: . А
именно:
Множества, построенные на
рисунке обладают целой размерностью. Зададимся вопросом, возможно
ли такое построение, при котором показатель  в равенстве (1) не
являлся целым, то есть такое, что при разбиении исходного
множества на в равенстве (1) не
являлся целым, то есть такое, что при разбиении исходного
множества на  непересекающихся подмножеств, полученных
масштабированием оригинала с коэффициентом непересекающихся подмножеств, полученных
масштабированием оригинала с коэффициентом  , значение , значение  не
будет выражаться целым числом. Ответ, как мы убедимся, - да! Такое
множество называют самоподобным фракталом. Величину не
будет выражаться целым числом. Ответ, как мы убедимся, - да! Такое
множество называют самоподобным фракталом. Величину 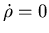 называют фрактальной размерностью или размерность подобия. Явное
выражение для
называют фрактальной размерностью или размерность подобия. Явное
выражение для 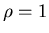 через через 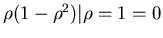 и и  находится логарифмированием
обеих частей:
Логарифм можно взять по любому
положительному основанию, отличному от единицы, например находится логарифмированием
обеих частей:
Логарифм можно взять по любому
положительному основанию, отличному от единицы, например
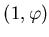 Нетрудно показать, что Нетрудно показать, что 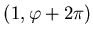 есть известная нам
размерность Хаусдорфа-Безиковича. есть известная нам
размерность Хаусдорфа-Безиковича.
Дадим теперь строгое определение самоподобия.
Определение. Будем называть компактное множество 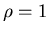 самоподобным, если существуют такие преобразования подобия
самоподобным, если существуют такие преобразования подобия
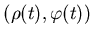 , что имеет место представление: , что имеет место представление:
Причем множества 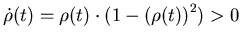 имеют мало общих точек.
имеют мало общих точек.
Теорема. Пусть 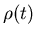 - самоподобное множество, то есть
выполняется (3), причем - самоподобное множество, то есть
выполняется (3), причем 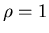 попарно не пересекаются.
Обозначим через попарно не пересекаются.
Обозначим через 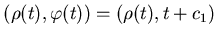 единственное решение уравнения:
где единственное решение уравнения:
где 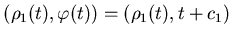 -
коэффициенты подобия. Тогда, если -
коэффициенты подобия. Тогда, если 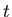 , то размерность
Хаусдорфа множества , то размерность
Хаусдорфа множества 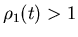 равна: равна:
Доказательство. Выберем такое малое положительное число
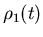 , чтобы дилатации , чтобы дилатации
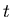 попарно не пересекались. Обозначим через
попарно не пересекались. Обозначим через
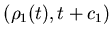 число
шаров радиуса число
шаров радиуса 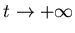 , необходимых для того, чтобы покрыть
множество , необходимых для того, чтобы покрыть
множество 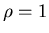 . Для . Для
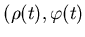 имеем: имеем:
Так как 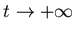 есть преобразование подобия с коэффициентом есть преобразование подобия с коэффициентом 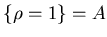 ,
то ,
то 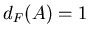 преобразует преобразует 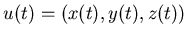 -покрытие множества -покрытие множества
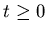 в в
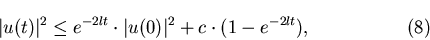 -покрытие
множества -покрытие
множества 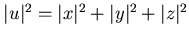 . Следовательно,
Перепишем (17) в виде: . Следовательно,
Перепишем (17) в виде:
С использованием (8):
где 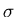 . Разделив на . Разделив на
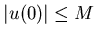 , получим уравнение
(4). , получим уравнение
(4).
Следствие. Если все коэффициенты подобия в теореме равны
между собой, то есть
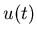 , то размерность
Хаусдорфа множества , то размерность
Хаусдорфа множества 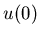 определяется из уравнения:
Если все коэффициенты подобия определяется из уравнения:
Если все коэффициенты подобия 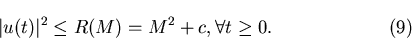 преобразований
преобразований 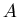 соответственно, лежат в интервале соответственно, лежат в интервале 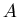 и
то решение уравнения
(4) называется размерностью подобия множества и
то решение уравнения
(4) называется размерностью подобия множества 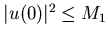 . При этом
не требуется, чтобы множества . При этом
не требуется, чтобы множества 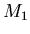 не пересекались. не пересекались.
Конечно, хотелось бы распространить теорему и на такие множества,
в представлении (3) которых множества 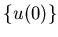 могли бы иметь
общие точки. Например, в случае ковра Серпинского вершины
центральных треугольников принадлежат сразу двум смежным
треугольникам. Эти пересечения, очевидно, незначительны и не
должны влиять на размерность всей фигуры. Можно доказать, что
достаточным условием применимости теоремы является равенство нулю могли бы иметь
общие точки. Например, в случае ковра Серпинского вершины
центральных треугольников принадлежат сразу двум смежным
треугольникам. Эти пересечения, очевидно, незначительны и не
должны влиять на размерность всей фигуры. Можно доказать, что
достаточным условием применимости теоремы является равенство нулю
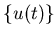 -меры Хаусдорфа пересечений, где -меры Хаусдорфа пересечений, где 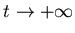 - размерность подобия - размерность подобия
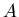 . Это условие выполняется всегда, когда множества . Это условие выполняется всегда, когда множества 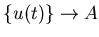 имеют лишь конечное или счетное число общих точек.
имеют лишь конечное или счетное число общих точек.
Таким образом, мы называем компактное множество 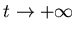 самоподобным,
если оно представимо в виде (3) и самоподобным,
если оно представимо в виде (3) и 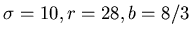 -мера Хаусдорфа всех попарных
пересечений множеств -мера Хаусдорфа всех попарных
пересечений множеств 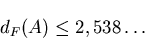 равна нулю, где равна нулю, где 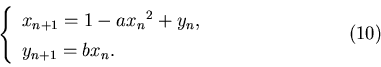 - размерность
подобия - размерность
подобия 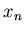 . .
|
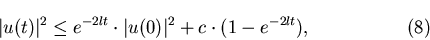 -покрытие
множества
-покрытие
множества