|
|
РАЗМЕРНОСТЬ ХАУСДОРФА dH
(ФРАКТАЛЬНАЯ РАЗМЕРНОСТЬ)
Как уже говорилось, точка имеет размерность равную нулю, отрезок,
окружность, вообще любая обычная кривая на плоскости или в
пространстве - размерность 1, круг, сфера - двумерны, тела -
трехмерны. Во всех перечисленных случаях размерность равна числу
независимых переменных, необходимых для того, чтобы задать точку
на рассматриваемом объекте. Однако смысл понятия ''размерность''
шире. Оно характеризует более ''тонкие'' топологические свойства
объектов и совпадает с числом независимых переменных, необходимых
для описания объекта, только в частных случаях. С одномерными
объектами мы связываем понятие длины, с двумерными площади и т.д.
Но как можно представить себе множество с размерностью 3/2? По
видимому, для этого требуется нечто промежуточное между длиной и
площадью, и если длину условно назвать 1-мерой, а площадь -
2-мерой, то требуется (3/2)-мера. В 1919 году Феликс Хаусдорф
действительно определил такую 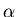 -меру для любого -меру для любого
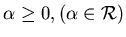 и на этой основе каждому
множеству в евклидовом пространстве сопоставил число, названное им
метрической размерностью. Идеи Хаусдорфа, не опубликовавшего
больше ни одной работы, в этом направлении, были развиты А.С.
Безиковичем, который длительное время был автором или соавтором
практически всех работ по данной тематике. В последующие годы
размерность Хаусдорфа-Безиковича получила применение в некоторых
узких областях математики, но ничто не предвещало той популярности
этого понятия за пределами математики, которая сейчас наблюдается. и на этой основе каждому
множеству в евклидовом пространстве сопоставил число, названное им
метрической размерностью. Идеи Хаусдорфа, не опубликовавшего
больше ни одной работы, в этом направлении, были развиты А.С.
Безиковичем, который длительное время был автором или соавтором
практически всех работ по данной тематике. В последующие годы
размерность Хаусдорфа-Безиковича получила применение в некоторых
узких областях математики, но ничто не предвещало той популярности
этого понятия за пределами математики, которая сейчас наблюдается.
Рассмотрим известные выражения для длины, площади и объема шара в
евклидовом пространстве. Диаметр (длина) шара радиуса 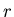 в в 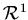 , составляет , составляет 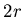 . Площадь шара в . Площадь шара в 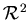 равна равна 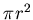 . Объём в . Объём в 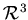 равен равен
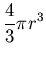 .
Сответствующие формулы в евклидовом пространстве любого целого
числа измерений хорошо известны: .
Сответствующие формулы в евклидовом пространстве любого целого
числа измерений хорошо известны:
где
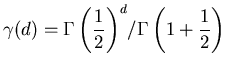 , а , а 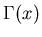 - гамма-функция
Эйлера: - гамма-функция
Эйлера:
Первый шаг в построении теории дробной размерности состоит в определении 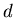 -меры шара
радиуса -меры шара
радиуса 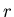 в в 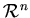 ,где ,где 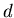 - любое неотрицательное вещественное число.
Это достигается путем распространения формулы (1)
на все вещественные - любое неотрицательное вещественное число.
Это достигается путем распространения формулы (1)
на все вещественные 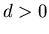 . Например мера шара в . Например мера шара в 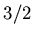 -мерном пространстве
опредляется как -мерном пространстве
опредляется как
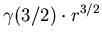 . .
Следующий шаг заключается в переносе понятия 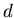 -меры с шара на
произвольное множество -меры с шара на
произвольное множество
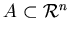 . Для этого построим
покрытие . Для этого построим
покрытие 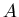 множеством шаров множеством шаров
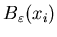 (рис.). (рис.).
Просуммируем их объемы:
Определение. 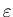 -фрактальной -фрактальной 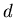 -мерой
множества называется число -мерой
множества называется число
или
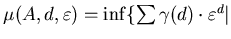 всевозможным покрытиям множества
всевозможным покрытиям множества  . .
Например, если
![$A_1=[0,1]\in R^1$](../HTML/dimH/img32.gif) , то , то
![$N(\varepsilon)=
\left[\displaystyle\frac{1}{2\varepsilon}\right]+1$](../HTML/dimH/img33.gif) . .
При
 этот этот  может только увеличиваться.
Следовательно, всегда существует предел может только увеличиваться.
Следовательно, всегда существует предел
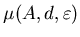 при при
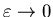 . .
Определение. Фрактальной 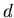 -мерной сферической мерой
Хаусдорфа называется число -мерной сферической мерой
Хаусдорфа называется число
Часто бывает:
Безикович показал, что для каждого 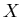 всегда существует число всегда существует число
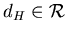 , что , что 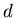 -мерная мера Хаусдорфа компакта -мерная мера Хаусдорфа компакта 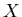 бесконечна при
бесконечна при 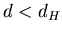 , и напротив равна 0, при , и напротив равна 0, при 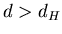 . .
Если
![$A_1=[0,1]$](../HTML/dimH/img47.gif) , то при , то при 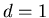 , ,
![$\mu_F(A_1,1)=\lim_{\varepsilon\to0+}
\varepsilon\cdot
N(\varepsilon)=\lim_{\var...
...n\cdot(\left[\displaystyle\frac{1}{2\varepsilon}\right]+1)=\displaystyle\frac12$](../HTML/dimH/img49.gif) В тоже время для
В тоже время для 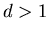
![$\mu_F(A_1,d)=\lim_{\varepsilon\to0+}\varepsilon^d\cdot(\left[\displaystyle\frac1{2\varepsilon}\right]+1)=0$](../HTML/dimH/img51.gif) .
А для .
А для 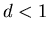
![$\mu_F(A_1,d)=\lim_{\varepsilon\to0+}\varepsilon^d\cdot(\left[\displaystyle\frac1{2\varepsilon}\right]+1)=+\infty$](../HTML/dimH/img53.gif)
В общем случае замкнутого ограниченного множества 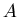 легко
видеть, что если легко
видеть, что если 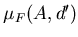
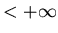 , то , то 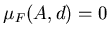 для
любого для
любого 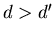 . Если же . Если же 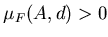 , то для , то для
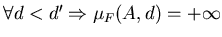 . Следовательно, существует
такое число . Следовательно, существует
такое число
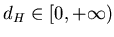 , что , что  при при 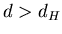 и и
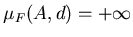 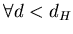 , в то время как , в то время как 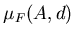 может быть любым числом из интервала
может быть любым числом из интервала ![$[0,+\infty]$](../HTML/dimH/img67.gif) . Очевидно, . Очевидно,
Определение. Число 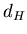 , удовлетворяющее соотношению: , удовлетворяющее соотношению:
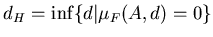 называется размерностью
Хаусдорфа-Безиковича (метрической или фрактальной размерностью)
множества называется размерностью
Хаусдорфа-Безиковича (метрической или фрактальной размерностью)
множества 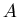 . Обозначается как . Обозначается как 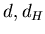 или или 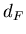 . .
Например, для ![$A_1=[0,1]$](../HTML/dimH/img74.gif)
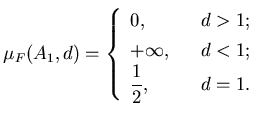 Значит, Значит, 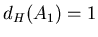 . .
Вернемся теперь к формуле (4):
Прологарифмируем обе части:
или
Для большинства ''хороших'' объектов, пространств, множеств 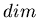 и
и 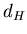 совпадают, однако существуют объекты для которых совпадают, однако существуют объекты для которых
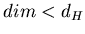 . Это и есть фракталы. . Это и есть фракталы.
|
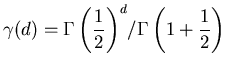 , а
, а 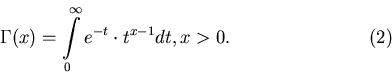

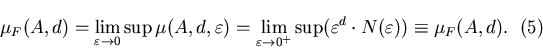
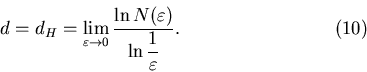

![$N(\varepsilon)=
\left[\displaystyle\frac{1}{2\varepsilon}\right]+1$](../HTML/dimH/img33.gif) .
.![$\mu_F(A_1,1)=\lim_{\varepsilon\to0+}
\varepsilon\cdot
N(\varepsilon)=\lim_{\var...
...n\cdot(\left[\displaystyle\frac{1}{2\varepsilon}\right]+1)=\displaystyle\frac12$](../HTML/dimH/img49.gif) В тоже время для
В тоже время для ![$\mu_F(A_1,d)=\lim_{\varepsilon\to0+}\varepsilon^d\cdot(\left[\displaystyle\frac1{2\varepsilon}\right]+1)=0$](../HTML/dimH/img51.gif) .
А для
.
А для ![$\mu_F(A_1,d)=\lim_{\varepsilon\to0+}\varepsilon^d\cdot(\left[\displaystyle\frac1{2\varepsilon}\right]+1)=+\infty$](../HTML/dimH/img53.gif)
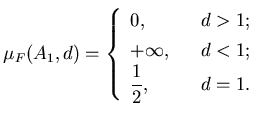 Значит,
Значит,